
еӨ§жҳҢеҚҺеҳү科еӯҰд»ӘеҷЁйғ?/p>
 зҷҪйҮ‘дјҡе‘ҳ
зҷҪйҮ‘дјҡе‘ҳ
 е·Іи®ӨиҜ?/p>
е·Іи®ӨиҜ?/p>
 жүӢжңәзүҮьimg class="sj_xl" src="//www.znpla.com/ruishihuajia/v2images/xia.png"/>
жүӢжңәзүҮьimg class="sj_xl" src="//www.znpla.com/ruishihuajia/v2images/xia.png"/>
жү«дёҖжү«пјҢжүӢжңәи®ҝй—®
 е…ідәҺжҲ‘们
е…ідәҺжҲ‘们
 еҠ е…Ҙ收и—Ҹ
еҠ е…Ҙ收и—Ҹ

еӨ§жҳҢеҚҺеҳү科еӯҰд»ӘеҷЁйғ?/p>
 зҷҪйҮ‘дјҡе‘ҳ
зҷҪйҮ‘дјҡе‘ҳ
 е·Іи®ӨиҜ?/p>
е·Іи®ӨиҜ?/p>
еӣәдҪ“жқҗж–ҷиЎЁйқўзҡ„зІҫзЎ®иЎЁеҫҒеңЁжқҗж–ҷзҡ„з ”з©¶е’Ңи®ёеӨҡе·Ҙдёҡдә§е“ҒејҖеҸ‘иҝҮзЁӢдёӯиө·зқҖиҮіе…ійҮҚиҰҒзҡ„дҪңз”ЁгҖӮжқҗж–ҷиЎЁйқўзҡ„ж¶Ұж№ҝжҖ§еңЁжІ№жјҶгҖҒеҚ°еҲ·е’Ңз”ҹзү©жқҗж–ҷдёҺз»Ҷиғһй—ҙзӣёдә’дҪңз”Ёзӯүз ”з©¶йўҶеҹҹдёӯеҗҢж ·жҳҜдёҖз§ҚйқһеёёйҮҚиҰҒзҡ„иЎЁеҫҒеҸӮж•°гҖӮеҸҜйҖҡиҝҮжөӢйҮҸж¶ІдҪ“дёҺеӣәдҪ“жқҗж–ҷй—ҙзҡ„жҺҘи§Ұи§’жқҘиЎЁеҫҒжқҗж–ҷзҡ„ж¶Ұж№ҝжҖ§гҖҒь/span>
иЎЁйқўиҮӘз”ұиғҪеҹәжң¬зҗҶи®№ь/span>
и‘—еҗҚзҡ„жқЁж°Ҹж–№зЁӢжҸҸиҝ°дәҶеӣ№ь/span>-ж¶ұь/span>-ж°”дёүзӣёжҺҘи§Ұзҡ„е№іиЎЎгҖӮе…·дҪ“е…¬ејҸеҰӮдёӢпјҡ
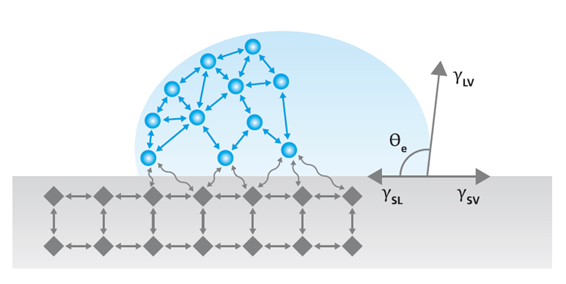
еӣҪь/span>1еӣәж¶Іж°”дёүзӣёзӮ№еҫҮь/span>
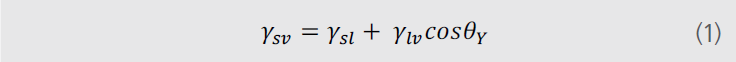
з•Ңйқўеј еҠӣОіsvгҖ?/span>Оіslе’Ӣь/span>Оіlvжһ„жҲҗе№іиЎЎпјҢж¶Ұж№ҝжҺҘи§Ұи§’пјҢеҚіжқЁж°ҸжҺҘи§Ұ觑ь/span>ОёYгҖӮжқЁж°Ҹж–№зЁӢеҒҮе®ҡеӣәдҪ“иЎЁйқўеҢ–еӯҰеқҮдёҖдё”е…үж»‘пјҢеҰӮжһңе®һйҷ…ж ·е“ҒиЎЁйқўжңүдёҖе®ҡзІ—зіҷеәҰпјҢеҲҷеҸҜд»ҘдҪҝз”ЁзІ—зіҷеәҰж ЎеҮҶжҺҘи§Ұи§’жқҘиҝӣиЎҢиЎЁеҫҒпјҢе…·дҪ“ж–№жі•дјҡеңЁеҗҺйқўзҡ„ж–Үз« дёӯжҢҮеҮәгҖҒь/span>
жҺҘи§Ұи§’зҡ„дёҖдёӘйҮҚиҰҒзҡ„еә”з”ЁжҳҜйҖҡиҝҮжөӢйҮҸжҺҘи§Ұи§’иғҪеӨҹи®Ўз®—еҮәеӣәдҪ“зҡ„иЎЁйқўиҮӘз”ұиғҪгҖӮиЎЁйқўиҮӘз”ұиғҪдёҺж¶ІдҪ“зҡ„иЎЁйқўеј еҠӣзҡ„еҚ•дҪҚеқҮдё№ь/span>mN/mпјҮь/span>=dynes/cmпјүгҖӮе°Ҫз®ЎжҺҘи§Ұи§’жң¬иә«иғҪеӨҹиЎЁеҫҒжқҗж–ҷиЎЁйқўзҡ„ж¶Ұж№ҝжҖ§пјҢдҪҶжҺҘи§Ұи§’зҡ„з»“жһңдёҺжөӢиҜ•зҡ„ж¶ІдҪ“жңүеҫҲеӨ§е…ізі»гҖҒь/span>
еңЁпјҲ1пјүж–№зЁӢдёӯпјҢиЎЁйқўиҮӘз”ұиғҪжҳҜйҖҡиҝҮжқҗж–ҷзҡ„жҺҘи§Ұи§’гҖҒж¶ІдҪ“иЎЁйқўеј еҠӣе’Ңеӣәж¶Ід№Ӣй—ҙзҡ„з•Ңйқўеј еҠӣи®Ўз®—еҫ—еҲ°зҡ„гҖӮеүҚдёӨиҖ…еҫҲе®№жҳ“еңЁе®һйӘҢдёӯиҺ·еҫ—пјҢе…ій”®зҡ„й—®йўҳжҳҜеӣәж¶Ій—ҙзҡ„з•Ңйқўеј еҠӣдёҚе®№жҳ“зӣҙжҺҘжөӢеҫ—гҖӮдёәдәҶи§ЈеҶіж–№зЁӢдёӯзҡ„иҝҷдёӘй—®йўҳпјҢеҝ…йЎ»иҰҒиҝӣиЎҢдёҖзі»еҲ—еҒҮе®ҡгҖӮе…ідәҺиЎЁйқўиҮӘз”ұиғҪзҡ„дёҖзі»еҲ—еҒҮе®ҡеә”иҝҗиҖҢз”ҹгҖҒь/span>
еҗёйҷ„е’Ңйҷ„зқҖ
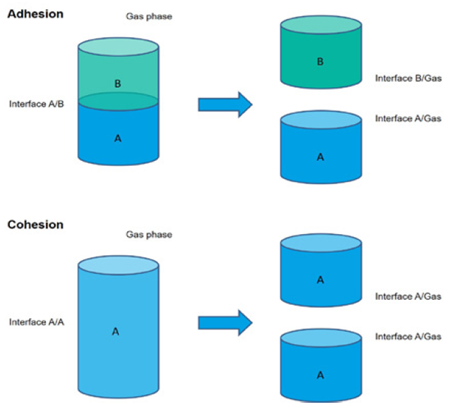
дёәиғҪдҫӣжӣҙжё…жҷ°зҡ„зҗҶи§ЈдёҚеҗҢзҡ„зҗҶи®әпјҢеҝ…йЎ»йҰ–е…Ҳи§ЈйҮҠдёӢвҖӣь/span>зІҳйҷ„еҠһь/span>вҖңь/span>зҡ„жҰӮеҝөгҖӮзғӯеҠӣеӯҰзІҳйҷ„жҳҜжҢҮе°ҶиЎЁйқўеҲҶжҲҗдёӨдёӘж–°иЎЁйқўжүҖйңҖиҰҒзҡ„еҠҹпјҢеҰӮеӣҫ2жүҖзӨәгҖӮзІҳйҷ„еҠҹж–№зЁӢеҰӮдёӢпјҷь/span>
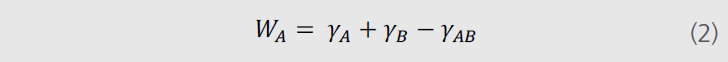
ж–№зЁӢпјҮь/span>2пјүдёӯзҡғь/span>ОіABдёәдёӨзӣёй—ҙзҡ„з•Ңйқўеј еҠӣпјҢОіAдё№ь/span>Aзӣёзҡ„иЎЁйқўеј еҠӣпјӢь/span>ОіBдё№ь/span>Bзӣёзҡ„иЎЁйқўеј еҠӣгҖӮеҰӮжһңе…¶д»–зӣёдёәеӣәдҪ“жҲ–иҖ…е…¶д»–ж¶ІдҪ“пјҢж–№зЁӢеҲҷж”№еҶҷжҲҗеҰӮдёӢеҪўејҸпјҷь/span>
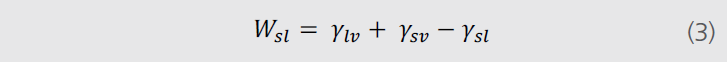
ж–№зЁӢпјҮь/span>1пјүе’Ңж–№зЁӢпјҮь/span>3пјүдҪ•д»ҘеҗҲ并жҲҗеҰӮдёӢж–№зЁӢпјҷь/span>

з”ЁеҗҢж ·зҡ„ж–№жі•йҷ„зқҖеҠҹзҡ„е®ҡд№үеҰӮеӣҫ2жүҖзӨәгҖҒь/span>

Berthelotең?/span>19дё–зәӘжң«zuiе…ҲдҪҝз”ЁиЎЁйқўиҮӘз”ұиғҪзҡ„и®Ўз®—ж–№жі•гҖӮд»–еҒҮе®ҡеӣәдҪ“е’Ңж¶ІдҪ“д№Ӣй—ҙзҡ„зІҳйҷ„еҠҹпјҲWAпјүзӯүдәҺеӣәдҪ“йҷ„зқҖеҠҹе’Ңж¶ІдҪ“йҷ„зқҖеҠҹзҡ„еҮ дҪ•е№іеқҮеҖјгҖҒь/span>
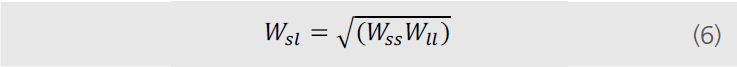
е°Ҷж–№зЁӢпјҲ4пјүгҖҒж–№зЁӢпјҲ5пјүе’Ңж–№зЁӢпјҮь/span>6пјүз»“еҗҮь/span>
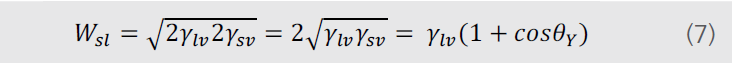
Berthelotзҡ„зҗҶи®әиғҢжҷҜдёәеҲҶеӯҗй—ҙзҡ„дјҰж•ҰдҪңз”ЁеҠӣпјҢеӣ жӯӨиЎЁйқўиҮӘз”ұиғҪзҗҶи®әдё»иҰҒйҒөеҫӘзҡ„жҳҜи¶…дёҙз•ҢжөҒдҪ“зҗҶи®әгҖҒь/span>
еӣҪь/span>2зІҳйҷ„е’Ңйҷ„зқҖ
иЎЁйқўиҮӘз”ұиғҪи®Ўз®—жЁЎеһҠь/span>
иЎ?/span>1иЎЁйқўиҮӘз”ұиғҪж–№жі•жҖ»з»“
OWRK/Fowkes
е°ҶиЎЁйқўиҮӘз”ұиғҪеҲ’еҲҶжҲҗдёҚеҗҢз»„еҲҶзҡ„жғіжі•еҒҮе®ҡдәҶеӣәж¶Ій—ҙз•Ңйқўеј еҠӣж•°еҖјеҸ–еҶідәҺжөӢиҜ•зҡ„еӣәдҪ“ж ·е“Ғе’Ңж¶ІдҪ“зҡ„з§Қзұ»гҖҒь/span>FowkesеҒҮе®ҡеӣәдҪ“зҡ„иЎЁйқўиҮӘз”ұиғҪпјҲж¶ІдҪ“зҡ„иЎЁйқўеј еҠӣпјүжҳҜеҚ•зӢ¬йғЁеҲҶзҡ„жҖ»е’ҢгҖҒь/span>
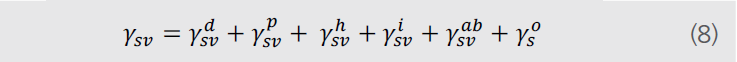
ОіsvdгҖ?/span>ОіsvpгҖ?/span>ОіsvhгҖ?/span>Оіsviе’Ӣь/span>ОіsvabеҲҶеҲ«жҳҜиүІж•ЈгҖҒжһҒжҖ§гҖҒж°ўгҖҒж„ҹеә”е’Ңй…ёзўұйғЁеҲҶгҖҒь/span>ОіsoиЎЁзӨәжүҖжңүе…¶д»–зҡ„зӣёдә’дҪңз”ЁгҖҒь/span>Fowkesдё»иҰҒжҳҜй’ҲеҜ№дәҺд»…д»…еҗ«жңүиүІж•ЈйғЁеҲҶзҡ„еӨҡз§Қзү©иҙЁпјҲеӣәдҪ“е’Ңж¶ІдҪ“пјүгҖӮж №жҚ?/span>FowkesиүІж•ЈдҪңз”ЁдёҺдјҰж•ҰеҠӣзҡ„дҪңз”ЁжҳҜз”ұз”өеӯҗеҒ¶жһҒеј•иө·зҡ„жіўеҠЁгҖҒь/span>Owenе’Ӣь/span>Wendtи·ҹйҡҸFowkesзҡ„жғіжі•з»§з»ӯиҝӣиЎҢйҳҗиҝ°ж–№зЁӢпјҲ8пјүдёӯйҷӨеҺ»ОіsvdеӨ–зҡ„жүҖжңүз»„еҲҶйғҪеҸҜд»Ҙе®ҡд№үдёәжһҒжҖ§йғЁеҲҶпјҢиҝӣиҖҢдә§з”ҹеҮәж–№зЁӢпјҮь/span>9пјүгҖҒь/span>
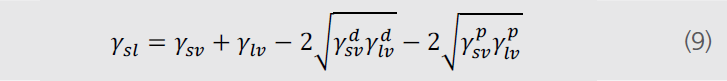
еҰӮжһңе°Ҷж–№зЁӢпјҲ4пјүдёҺдёҠиҝ°ж–№зЁӢз»“еҗҲпјҢеҲҷж”№еҶҷеҗҺзҡ„ж–№зЁӢз§°дёәWORKгҖҒь/span>

ж–№зЁӢпјҮь/span>10пјүдёӯжңүдёӨдёӘжңӘзҹҘйЎ№Оіsvdе’Ӣь/span>ОіsvpпјҢйңҖиҰҒиүІж•Је’ҢжһҒжҖ§з»„еҲҶе·ІзҹҘзҡ„дёӨз§Қж¶ІдҪ“жқҘи§ЈеҶіиҝҷдёӘй—®йўҳгҖӮжөӢиҜ•ж—¶йңҖйҖүжӢ©дё»жү“жһҒжҖ§е’Ңдё»жү“иүІж•ЈйғЁеҲҶзҡ„дёӨз§Қж¶ІдҪ“гҖӮж°ҙгҖҒз”ҳжІ№е’Ңз”Ій…°иғәеҸҜдҪңдёәжһҒжҖ§ж¶ІдҪ“пјҢдә зў з” зғ·е’ҢОұ-жәҙиҗҳеҸҜдҪңдёәиүІж•Јж¶ІдҪ“гҖӮж°ҙеҫҲжҳҫ然жһҒжҖ§ж•°еҖјеҫҲеӨ§пјҢеҸҜд»Ҙж»Ўи¶ідҪҝ用并且жҳҜж— жұЎжҹ“зҡ„ж¶ІдҪ“гҖӮеҜ№дәҚь/span>sesameйӮЈйғЁеҲҶзҡ„ж¶ІдҪ“зҡ„йҖүжӢ©зӣёеҜ№жқҘиҜҙдјҡжӣҙеӨҚжқӮдёҖдәӣгҖӮеӨ§йғЁеҲҶиүІж•Јж¶ІдҪ“зҡ„иЎЁйқўеј еҠӣеҫҲдҪҺпјҢеңЁеӨ§йғЁеҲҶеӣәдҪ“иЎЁйқўзҡ„жҺҘи§Ұи§’ж•°еҖјеҮ д№Һдёә0В°гҖӮеӣ жӯӨйңҖиҰҒжӣҙеҠ зү№ж®Ҡзҡ„ж¶ІдҪ“жҺўй’ҲгҖҒь/span>OWRKжЁЎеһӢжҳҜжңҖдёәеёёз”Ёзҡ„иЎЁйқўиҮӘз”ұиғҪи®Ўз®—жЁЎеһӢгҖҒь/span>

Wu
WuжЁЎеһӢеҸ—еҲ°Owenе’Ӣь/span>Wendtзҡ„еҪұе“ҚпјҢд№ҹе°ҶиЎЁйқўиҮӘз”ұиғҪеҲҶжҲҗжһҒжҖ§йғЁеҲҶе’ҢиүІж•ЈйғЁеҲҶгҖҒь/span>WuжЁЎеһӢ并没жңүдҪҝз”ЁеҮ дҪ•е№іеқҮж•°пјҮь/span>10пјүи®Ўз®—иҖҢжҳҜдҪҝз”ЁдәҶи°ғе’Ңе№іеқҮж•°пјҮь/span>11пјүиҝӣиЎҢи®Ўз®—зҡ„гҖҒь/span>
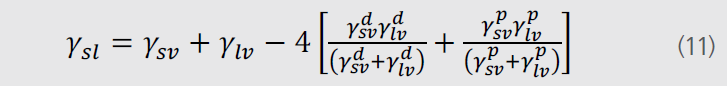
еҰӮжһңе°Ҷж–№зЁӢпјҲ11пјүдёҺж–№зЁӢпјҮь/span>4пјүз»“еҗҲеҲҷж–№зЁӢеҸҜж”№еҶҷжҲҗеҰӮдёӢеҪўејҸпјҷь/span>
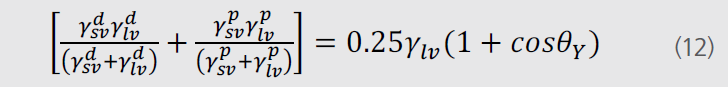
Wuж–№жі•йңҖиҰҒиҮіе°‘дёӨз§Қж¶ІдҪ“иҝӣиЎҢжөӢиҜ•пјҢдёҖз§ҚжһҒжҖ§ж¶ІдҪ“дёҖз§ҚиүІж•Јж¶ІдҪ“пјҢжңҖеёёз”Ёзҡ„д»Қ然жҳҜж°ҙе’Ңдә зў з” зғ·гҖҒь/span>
Wuж–№зЁӢзҡ„дё»иҰҒдҫқжҚ®жқҘжәҗдәҺзҗҶи®әзҶ”иһҚиҒҡеҗҲзү©зҡ„е®һйӘҢжөӢйҮҸгҖҒь/span>
Wuдҝ®жӯЈдәҶеҮ дҪ•е№іеқҮж•°дёӯеҝҪи§Ҷзҡ„жһҒжҖ§й—ҙзҡ„зӣёдә’дҪңз”ЁгҖҒь/span>

Acid-base
Acid-baseжЁЎеһӢжҳҜиҝ‘жңҹе…ҙиө·зҡ„иЎЁйқўиҮӘз”ұиғҪи®Ўз®—жЁЎеһӢгҖҒь/span>Van OssпјӢь/span>Goodе’Ӣь/span>ChaudhuryдёүиҖ…жҸҗеҮәиЎЁйқўиҮӘз”ұиғҪеҸҜеҲҶдёәиҝңи·қзҰ»зҡ„иҢғеҫ·еҚҺеҠӣзӣёдә’дҪңз”Ёе’Ңзҹӯи·қзҰ»зҡ„жһҒжҖ§зӣёдә’дҪңз”ЁгҖӮйҡҸеҗҺпјҢзӣёеҗҢзҡ„дҪңиҖ…д№ҹжҢҮеҮәпјҢе°Ҫз®ЎеӨ§йғЁеҲҶжһҒжҖ§дҪңз”ЁжҳҜеҸ‘з”ҹеңЁдёҙиҝ‘еҲҶеӯҗд№Ӣй—ҙпјҢиғҪеӨҹйҖҡиҝҮеҗёеј•жқҘж”№еҸҳеҲҶеӯҗйЎәеәҸпјҢеҸҜж”№еҸҳеҮ дёӘз»“еҗҲеҲҶеӯҗзҡ„зӣҙеҫ„гҖӮеҸҜд»ҘжҳҺзЎ®дёҖзӮ№пјҢжҳҜдҪҝз”ЁдёҠж Ҷь/span>Aе’Ӣь/span>BжқҘд»Јжӣҝи·Ҝжҳ“ж–Ҝй…ёзўұзҡ„зӣёдә’дҪңз”ЁгҖӮйҖҡиҝҮдҪҝз”ЁAcid-baseжЁЎеһӢж–№зЁӢеҰӮдёӢжүҖзӨәпјҡ
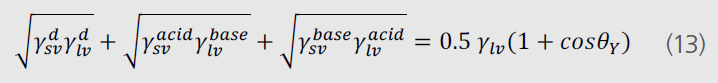
з”ұдёҠиҝ°еҸҜд»ҘзңӢеҮәй•ҝи·қзҰ»иҢғеҫ·еҚҺеҠӣдёҺиүІж•ЈдҪңз”ЁзӣёеҗҢгҖҒь/span>
дёҠиҝ°ж–№зЁӢпјҮь/span>13пјүдёӯжңүдёүз§ҚдёҚзЎ®е®ҡйЎ№пјҢеӣ жӯӨйңҖиҰҒдёүз§Қж¶ІдҪ“иҝӣиЎҢжөӢиҜ•пјҢ1з§ҚиүІж•Јж¶ІдҪ“е’Ң2з§ҚжһҒжҖ§ж¶ІдҪ“гҖҒь/span>
еңЁеҲҶеҲ«д»Ӣз»Қе°ҶжһҒжҖ§з»„еҲҶеҲҶжҲҗз”өеӯҗдҫӣдҪ“е’Ңз”өеӯҗеҸ—дҪ“еҗҺпјҢе°ұеҫҲе®№жҳ“зҗҶи§Ји®ёеӨҡжңүжңәй«ҳеҲҶеӯҗжқҗж–ҷе°Өе…¶жҳҜжһҒжҖ§з”ҹзү©й«ҳеҲҶеӯҗпјҢдё»иҰҒжҲ–иҖ…еҸӘжҳҜз”өеӯҗдҫӣдҪ“жҲ–иҖ…жһҒе°‘йғЁеҲҶд»…д»…жҳҜз”өеӯҗеҸ—дҪ“гҖӮиЎЁйқўд»…д»…жҳҜз”өеӯҗдҫӣдҪ“жҲ–иҖ…з”өеӯҗеҸ—дҪ“еҲҷеҸ«еҒҡеҚ•дёҖжһҒжҖ§гҖӮиҝҷж ·зҡ„еҚ•дёҖжһҒжҖ§иЎЁйқўжңүи®ёеӨҡж„ҸжғідёҚеҲ°зҡ„жҖ§иҙЁпјҢеҸҜд»Ҙи§ЈйҮҠдёҖдәӣйҡҫд»ҘзҗҶи§Јзҡ„иғ¶дҪ“е’ҢиЎЁйқўзҡ„зҺ°иұЎгҖҒь/span>Acid-baseжЁЎеһӢиғҪеӨҹжҸҗдҫӣзЁіе®ҡзҡ„жөӢиҜ•з»“жһңгҖҒь/span>
дҪҝз”ЁAcid-baseзҗҶи®әзҡ„йҡҫзӮ№жҳҜжІЎжңүд»»дҪ•е·ІзҹҘй…ёзўұз»„еҲҶзҡ„ж¶ІдҪ“гҖӮеҸҜдј°и®Ўй…ёзўұжҜ”зҺҮпјҢжһҒжҖ§йғЁеҲҶеҸҜдҪҝз”ЁжҺҘи§Ұи§’ж–№жі•жөӢе®ҡпјҢеҰӮз”ҳжІ№е’Ңз”Ій…°иғәж»ҙеңЁеҚ•дёҖжһҒжҖ§зҡ„иЎЁйқўеҰҒь/span>PMMAгҖҒь/span>
й’ҲеҜ№иҜҘжЁЎеһӢзҡ„дё»иҰҒдәүи®®еңЁдәҺй…ёжҖ§е’ҢзўұжҖ§з»„еҲҶзҡ„з•Ңйқўеј еҠӣеҖјеҫҲжңүеҸҜиғҪжҳҜиҙҹеҖјгҖӮиүІж•ЈйғЁеҲҶдёҚиғҪеӨҹе°ҸдәҺ0пјҢдҪҶеҰӮжһңжҳҜй…ёзўұз»„жҲҗжқЎд»¶жҳҜзЎ®е®ҡзҡ„жғ…еҶөдёӢд№ҹжңүеҸҜиғҪжҳ?/span>0гҖӮз”ұжӯӨеҲҷдјҡеј•еҸ‘дёҖдёӘи®Ёи®әпјҡеҰӮдҪ•йҖүжӢ©жөӢиҜ•ж¶ІдҪ“пјҢдёӢеҲ—ж¶ІдҪ“еқҮеҸҜдҪҝз”ЁпјҢж°ҙпјҢз”ҳжІ№пјҢдәҢ зў з” зғ·пјҢз”Ій…°иғәе’ҢОұ-жәҙиҗҳгҖҒь/span>
Schultz 1&2
SchultzжЁЎеһӢиғҪеӨҹж»Ўи¶ій«ҳиғҪиЎЁйқўзҡ„иЎЁйқўиҮӘз”ұиғҪзҡ„и®Ўз®—гҖӮе°Ҫз®Ўд»Һж–№жі•и§’еәҰжқҘиҜҙд№ӢеүҚиҜҙзҡ„ж–№жі•д№ҹеҸҜд»ҘдҪҝз”ЁпјҢдҪҶй—®йўҳеңЁдәҺй«ҳиғҪиЎЁйқўйҮҮз”ЁжҺҘи§Ұи§’ж–№жі•еҫҲеҸҜиғҪж•°еҖјеҫҲдҪҺжҲ–иҖ…жҺҘиҝ‘дәҺ0гҖӮеңЁиҝҷз§Қжғ…еҶөдёӢеҫҲе°Ҹзҡ„иҜҜе·®дјҡдҪҝз»“жһңжңүеҫҲеӨ§еҒҸе·®гҖӮеҮәдәҺиҝҷз§ҚеҺҹеӣҹь/span>SchultzжЁЎеһӢжҢҮеҮәдәҶйңҖиҰҒе°ҶеӣәдҪ“жөёж¶ҰеҲ°е…¶д»–ж¶ІдҪ“йҮҢйқўеҶҚз”Ёе…¶д»–ж¶ІдҪ“иҝӣиЎҢжҺҘи§Ұи§’жөӢиҜ•гҖҒь/span>
SchultzжЁЎеһӢиҝҳеҸҜеҲҶжҲҗдёӨз§ҚжЁЎеһӢпјӢь/span>Schultz1е’Ӣь/span>2гҖҒь/span>Schultz1жҳҜе°ҶеӣәдҪ“жөёж¶ҰеҲ°йқһжһҒжҖ§ж¶ІдҪ“йҮҢйқўеҶҚз”ЁжһҒжҖ§ж¶ІдҪ“иҝӣиЎҢжҺҘи§Ұи§’зҡ„жөӢиҜ•пјҢSchultz2еҲҷдёҺSchultz1е®Ңе…ЁзӣёеҸҚпјҢдҪҝз”ЁжҚ•жіЎжі•иҝӣиЎҢжҺҘи§Ұи§’зҡ„жөӢиҜ•пјҢеҰӮеӣҪь/span>3жүҖзӨәгҖҒь/span>
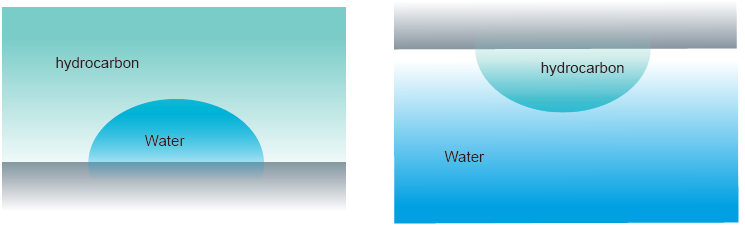
еӣҪь/span>3е·Ұиҫ№дё№ь/span>Schultz1пјҢеҸіиҫ№дёәSchultz2
з”ұдәҺжҺҘи§Ұи§’жөӢиҜ•иҝҮзЁӢдёӯжңүдёӨз§Қж¶ІдҪ“зҡ„еӯҳеңЁпјҢйңҖиҰҒиҖғиҷ‘ж¶ІдҪ“е’ҢеӣәдҪ“д№Ӣй—ҙзҡ„зӣёдә’дҪңз”ЁгҖҒь/span>
зўіж°ўеҢ–еҗҲзү©е’ҢеӣәдҪ“д№Ӣй—ҙзҡ„зӣёдә’дҪңз”ЁеҸҜеҶҷдҪңеҰӮдёӢж–№зЁӢпјҷь/span>
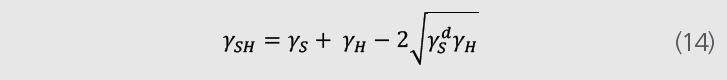
S=еӣәдҪ“пјӢь/span>H=зўіж°ўеҢ–еҗҲзү©гҖӮз”ұдәҺзўіж°ўеҢ–еҗҲзү©жІЎжңүи®°жҖ§з»„еҲҶпјҢйӮЈд№ҲжһҒжҖ§дҪңз”Ёдёә0гҖҒь/span>
ж°ҙе’ҢеӣәдҪ“й—ҙзҡ„зӣёдә’дҪңз”ЁеҸҜеҶҷжҲҗеҰӮдёӢеҪўејҸпјҡ

W=ж°ҙгҖҒь/span>
еӣәж¶Іж°”дёүиҖ…дҪҝз”Ёзҡ„жқЁж°Ҹж–№зЁӢеҰӮдёӢжүҖзӨәпјҡ
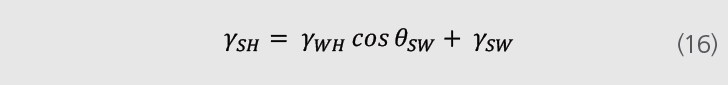
е°Ҷж–№зЁӢпјҲ14пјүпјҲ15пјүе’ҢпјҮь/span>16пјүз»“еҗҲеҸҜеҫ—еҲ°еҰӮдёӢж–№зЁӢпјҷь/span>
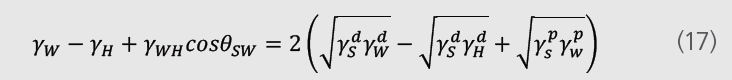
з”ұдәҺж–№зЁӢдёӯеҢ…еҗ«ж°ҙе’Ңзўіж°ўеҢ–еҗҲзү©й—ҙзҡ„з•Ңйқўеј еҠӣпјҢиҜҘж•°еҖјйңҖиҰҒжөӢе®ҡеҫ—еҲ°гҖҒь/span>
Schultzдё»иҰҒй’ҲеҜ№дәҺй«ҳиғҪеӣәдҪ“иЎЁйқўпјҢеҰӮйҮ‘еұһгҖҒйҮ‘еұһж°§еҢ–зү©е’ҢзҺ»з’ғзӯүгҖҒь/span>
EOSжЁЎеһӢ
е°Ҫз®ЎзҠ¶жҖҒж–№зЁӢжңүеҫҲеӨҡдёҚеҗҢзҡ„еҪўејҸпјҢеҒҡе№ҝдёәзҶҹзҹҘзҡ„жҳ?/span>NeumannжҸҗеҮәзҡ„ж–№зЁӢпјҢеҰӮдёӢжүҖзӨәпјҡ

еҪ“дёӯзҡ„еёёж•?/span>ОІ=0.0001247жҳҜйҖҡиҝҮе®һйӘҢзЎ®е®ҡзҡ„гҖӮиҜҘжЁЎеһӢеҸӘйңҖдҪҝз”ЁдёҖз§Қж¶ІдҪ“гҖӮй’ҲеҜ№дәҺиҜҘжЁЎеһӢзӣ®еүҚд№ҹжңүдёҖдәӣдәүи®®пјҢдәүи®®ж¶үеҸҠеҲ°еёёж•?/span>ОІжҳҜеҗҰдјҡжҒ’е®ҡдёҚеҸҳзҡ„пјӣзҠ¶жҖҒж–№зЁӢ并没жңүе°ҶиЎЁйқўеј еҠӣеҲҶжҲҗдёҚеҗҢзҡ„йғЁеҲҶпјӣзҠ¶жҖҒж–№зЁӢеҜ№дәҺжөӢиҜ•ж¶ІдҪ“зҡ„зәҜеәҰиҰҒжұӮйқһеёёй«ҳпјӣзҠ¶жҖҒж–№зЁӢдёҚиғҪеӨҹеғҸжқЁж°ҸжҺҘи§Ұи§’дёҖж ·йҖҡиҝҮзғӯеҠЁеҠӣеӯҰж–№жі•и§ЈйҮҠеүҚиҝӣи§’гҖҒь/span>
ZismanжӣІзәҝжЁЎеһӢ
ZismanжЁЎеһӢдё»иҰҒй’ҲеҜ№ж¶ІдҪ“е’ҢеӣәдҪ“й—ҙжҺҘи§Ұи§’жҺҘиҝҗь/span>0В°зҡ„жғ…еҶөгҖӮиЎЁйқўеј еҠӣзҡ„ж•°еҖјдёҺиЎЁйқўиҮӘз”ұиғҪдёҚеҗҢзҡ„жҳҜпјҢ并没жңүе°Ҷе…¶еҲҶжҲҗжһҒжҖ§е’ҢиүІж•ЈйғЁеҲҶгҖӮе®һйҷ…дёҠпјҢиЎЁйқўеј еҠӣжҳҜйҖҡиҝҮжөӢе®ҡеҗҢдёҖиЎЁйқўе’ҢдёҚеҗҢж¶ІдҪ“д№Ӣй—ҙзҡ„жҺҘи§Ұи§’иҺ·еҫ—зҡ„гҖҒь/span>COSОёдё№ь/span>YиҪҙпјҢиЎЁйқўеј еҠӣжҳ?/span>XиҪҙгҖҒь/span>

еӣҪь/span>4 ZismanжӣІзәҝжЁЎеһӢ
йқһзҗҶжғіиЎЁйқўзҡ„иЎЁйқўиҮӘз”ұиғјь/span>
иЎЁйқўиҮӘз”ұиғҪйҖҡиҝҮжқЁж°Ҹж–№зЁӢжөӢиҜ•зҡ„жҺҘи§Ұи§’жқҘзЎ®е®ҡгҖӮжқЁж°Ҹж–№зЁӢжҳҜеҒҮе®ҡеӣәдҪ“иЎЁйқўдёәзҗҶжғіиЎЁйқўпјҢзҗҶжғіиЎЁйқўж„Ҹе‘ізқҖеҢ–еӯҰе’ҢеҪўиІҢеқҮдёҖгҖӮ然иҖҢе®һйҷ…дёҠеҫҲйҡҫжүҫеҲ°зҗҶжғіиЎЁйқўпјҢиЎЁйқўжҲ–еӨҡжҲ–е°‘йғҪдјҡжңүзІ—зіҷеәҰзҡ„гҖӮеҰӮжһңйҖҡиҝҮжҺҘи§Ұи§’и®Ўз®—иЎЁйқўиҮӘз”ұиғҪиҖҢжІЎжңүе°ҶеӣәдҪ“иЎЁйқўзҡ„зІ—зіҷеәҰиҖғиҷ‘иҝӣеҺ»зҡ„иҜқпјҢиЎЁйқўиҮӘз”ұиғҪзҡ„ж•°еҖјжҳҜдёҚеҮҶзЎ®зҡ„гҖӮеӣ жӯӨй’ҲеҜ№зІ—зіҷиЎЁйқўе»әи®®дҪҝз”ЁзІ—зіҷеәҰж ЎеҮҶжҺҘи§Ұи§’жқҘи®Ўз®—иЎЁйқўиҮӘз”ұиғҪгҖҒь/span>
жҖ»з»“
жң¬ж–Үд»Ӣз»ҚдәҶеҮ з§Қеёёи§Ғзҡ„иЎЁйқўиҮӘз”ұиғҪжЁЎеһӢгҖӮиЎЁйқўиҮӘз”ұиғҪеҸҜж №жҚ®жһҒжҖ§зӣёдә’дҪңз”ЁеҲҶжҲҗдёҚеҗҢзҡ„з»„еҲҶгҖӮ然иҖҢпјҢд»Қ然жңүеҫҲеӨҡзҗҶи®әдёҠзҡ„й—®йўҳйңҖиҰҒеҺ»жҺўи®ЁгҖӮжң¬ж–Ү并дёҚиғҪеӨҹе»әи®®йӮЈз§ҚжЁЎеһӢжӣҙеҘҪпјҢж–Үз« ејҖе§ӢеӨ„зҡ„иЎЁдёӯжҖ»з»“дәҶеҗ„жЁЎеһӢзҡ„зү№зӮ№еҸҠдјҳзӮ№гҖӮеңЁе®һйҷ…иҝҮзЁӢдёӯе»әи®®еҰӮжһңйңҖиҰҒж•°жҚ®жҜ”еҜ№зҡ„иҜқпјҢе°ҪйҮҸдҪҝз”ЁеҗҢдёҖз§ҚжЁЎеһӢиҝӣиЎҢиЎЁйқўиҮӘз”ұиғҪзҡ„и®Ўз®—гҖҒь/span>
жӣҙеӨҡеҶ…е®№пјҢе…іжі?/span>вҖӣь/span>еӨ§жҳҢеҚҺеҳү科еӯҰд»ӘеҷЁйғ?/span>вҖңь/span>еҫ®дҝЎе…¬дј—еҸ¶ь/span>
зӣёе…ідә§е“Ғ
жӣҙеӨҡ
зӣёе…іж–Үз«
жӣҙеӨҡ
жҠҖжңҜж–Үз«ҹь/p>2024-10-09
жҠҖжңҜж–Үз«ҹь/p>2024-08-10
жҠҖжңҜж–Үз«ҹь/p>2024-05-30
жҠҖжңҜж–Үз«ҹь/p>2024-05-30
 жүӢжңәзүҲпјҡ
жүӢжңәзүҲпјҡ