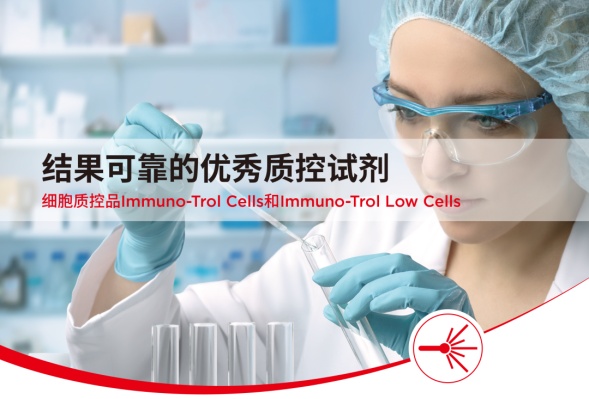
白金会员
白金会员
 已认�?/p>
已认�?/p>
转头的k 倻�/span>
转头的k 值(又称k 因子或k 系数)用以衡量转头的沉淀效率。所有的离心机厂家在转头出厂时都计算了制备型转头的k 值,转头k 值通过在转头运行至最高转速、离心管装满样品时计算得到的,其计算公式如下9�/span>
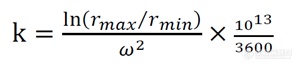
k � 转头的k 倻�/span>
rmax� 最大半径,指旋转轴到离心管底端的垂直距禺�/span>
rmin� 最小半径,指旋转轴到离心管顶端的垂直距禺�/span>
ω � 角速度
由于
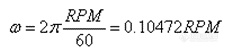
将公式(2)代入公式(1)可得到以下转头k 值的计算公式9�/span>
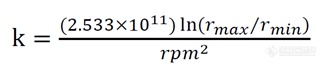
由上得出转头k 值是与转头的最高转逞�/span>咋�span style="font-size: 16px; line-height: 17.12px;">形状有关、�/span>
最高转速完全一样的转头,离心管与轴的角度越小,也就是rmax / rmin 越小,k 值就越小。所以制备型超速离心机的四类转头的k值如下:水平转头k �?nbsp;> 定角转头k �?nbsp;> 近垂直转头k �?nbsp;> 垂直转头k 值、�/span>
如果在离心时,转头没有运行到最高转速,那么rpm 就不能使用最高转速的k 值,必须将转头实际运行转速代入公式(3)来计算实际的k 值、�/span>

离心时间
已知某转头k 值和颗粒的沉降系数,可以计算出用该转头分离颗粒时所需要的时间。其公式如下9�/span>
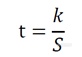
t � 沉淀时间(单位:小时(�/span>
k � 指实际运行状态下的转头k 倻�/span>
S � 颗粒的沉降系�?/span>
由公式(5)可以看出,转头k 值是评估转头离心效率的一个指标,对于沉淀同一颗粒,转头k 值越小,颗粒沉淀所需要的时间就越短,也就是离心效率越高;反之,转头k 值越大,颗粒沉淀所需要的时间就越长,转头的离心效率越低、�/span>
举例:分离沉降系数为 15 S 的蛋白,如果用的转头k 值是15,那么沉降该蛋白颗粒所需要的时间是:
t = k/s = 15/15 = 1 小时
如果用的转头k 值是18,那么沉降所需的时间是9�/span>
t = k/s = 18/15 = 1.2 小时
已知一个转头k 值和沉淀所需要的时间,如果用另一个转头来沉淀同样的颗粒,可以用以下公式来计算需要沉淀的时间:
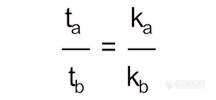
ka �?nbsp;a 转头的k 倻�/span>
kb �?nbsp;b 转头的k 倻�/span>
ta �?nbsp;a 转头沉降样品所需要的时间
tb �?nbsp;b 转头沉降样品所需要的时间
如果该转头不是在最高转速下运行,或者样品没有装满,又或者换用了其他更小的离心管(例如g-MAX 管等),相应k 值都会发生改变,相应离心所需的时间也需要重新计算、�/span>
综上所述,k 因子已经综合考虑了离心的转速、相对离心力以及样品在最小半径和最大半径等位置的受力改变情况,还有颗粒沉降的行程等因素,是计算离心时间、评价转头离心效率的最准确和最重要指标、�/span>
关注小贝离心课堂,了解更多离心信息!